Nasi Goreng Kambing
(Lamb/Ghoat Fried Rice)
Bahan-bahan
400 gr nasi putih75 gr daging kambing muda, iris tipis
40 gr nanas, potong dadu
2 siung bawang putih, cincang halus
1 bawang bombay, cincang halus
5 sdm minyak goreng
1 sdt ketumbar bubuk
2 cm kunyit, dihaluskan
2 kapulaga
25 gr daun bawang, iris halus
1-2 sdt garam
1 sdt merica bubuk
Cara Membuat
Lumuri daging kambing dengan campuran kunyit dan ketumbar dengan rata, biarkan beberapa menit agar meresap.Panaskan minyak, masukkan daging kambing, masak hingga 3/4 matang.
Masukkan bawang putih, bawang bombay dan kapulaga, aduk-aduk sebentar.
Masukkan buah nanas dan nasi, aduk hingga tercampur rata.
Taburkan daun bawang, garam dan merica, aduk lagi hingga rata.
Sajikan dengan irisan mentimun dan tomat.
Nasi Goreng Cumi Asam Manis
(Sweet-Sour Squid Fried Rice)
Bahan-bahan
1 piring nasi putih100 gram kismis
3 ekor cumi, bersihkan lalu iris-iris kecil
1 bawang bombay, cincang
3 siung bawang putih, iris halus
1 sdm pasta tomat
1 sdm air jeruk nipis
2 sdm minyak goreng
2 sdm saus tiram
1 sdt peterseli cincang
1/2-1 sdt garam
1/2 sdt merica
Cara Membuat
Panaskan minyak, tumis bawang bombay dan bawang putih hingga berbau sedap.Masukkan irisan cumi, aduk sebentar.
Masukkan nasi, pasta tomat, kismis, saus tiram, air jeruk nipis dan peterseli cincang. Aduk-aduk sampai rata.
Beri garam dan merica, aduk rata.
Angkat dan cetak nasi goreng dalam mangkuk, hidangkan bersama irisan tomat dan metimun.
Nasi Goreng Keju Istimewa
(Special Cheese Fried Rice)
Bahan-bahan
500 gr nasi putih250 gr dada ayam, potong dadu kecil
2 sdm mentega
200 gr keju, potong dadu kecil
4 sdm kacang polong
1/2 sdm kecap manis
1 bawang bombay, cincang halus
1 sdt garam
4 sosis sapi, iris tipis
4 sdm saus tomat
1 sdt kecap beraroma
1 batang wortel, potong dadu kecil rebus matang
Pelengkap
50 gr keju parut1/2 sdt garam
4 butir telur
Kocok, buat dadar dan iris tipis
Cara Membuat
Panaskan mentega, tumis bawang bombay, cabai merah, wortel, dada ayam dan sosis sapi hingga matang. Masukkan kacang polong, nasi putih, saus tomat, kecap manis, kecap beraroma dan garam. Aduk rata. Hidangkan selagi panas denga dadar keju.Nasi Goreng Oriental
(Oriental Fried Rice)
Bahan-bahan
1 piring nasi putih70 gr daging ayam
4 siung bawang putih
4 ekor udang
1 btr telur
2 bh cabai merah
50 gr bawang bombay
50 gr wortel
1 bt daun bawang
garam dan merica halus secukupnya
Cara Membuat
Udang dan daging ayam dipotong-potong. Telur ayam dikocok. Cabai merah dibuang isinya, lalu direbus, ,tiriskan lalu dihaluskan bersama bawang putih (diblender). Bawang bombay, wortel dan daun bawang diris-iris kecil.Semua bahan ditumis bersama-sama, beri garam, merica dan nasi putih. Kemudian diaduk sampai tercampur, lalu angkat. Pindahkan pada sebuah mangkuk (dicetak), lalu tuang pada sebuah piring.
Sajikan bersama irisan mentimun.
Nasi Goreng Sea Food
(Sea Food Fried Rice)
Bahan-bahan
2 piring nasi5 siung bawang putih, dirajang halus
25 gr udang
25 gr cumi-cumi
25 gr ikan kakap
1 sendok makan saos tomat
5 sendok makan minyak goreng
1 sendok makan kecap manis
1 sendok makan saos tiram
10 buncis dirajang halus
10 gr bawang pre
1 telur ayam, dikocok
10 gr kacang polong
merica sesuai selera
garam sesuai selera
Cara Membuat
Panaskan minyak goreng, tumis bawang putih dan bawang pre sampai harum, masukkan telur ayam yang dikocok.Masukkan udang, cumi-cumi, dan ikan kakap, masak hingga matang. Tambahkan nasi putih dan buncis, goreng sampai tercampur rata.
Tambahkan saos tomat, saus tiram, garam, merica, kecap manis, aduk hingga rata.
Tambahkan buncis, kacang polong, aduk hingga nasi goreng matang.
Nasi goreng siap dihidangkan dihias dengan irisan tomat, irisan mentimun dan daun sla.
Selamat mencoba...



 (dalam tulisan ini tetap digunakan yang terakhir), di mana konstanta
(dalam tulisan ini tetap digunakan yang terakhir), di mana konstanta 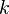 tersebut bernilai
tersebut bernilai 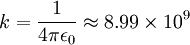

 akibat adanya sebuah titik muatan
akibat adanya sebuah titik muatan  yang terletak di
yang terletak di  digunakan rumus
digunakan rumus 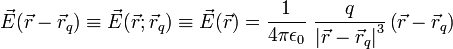
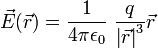
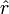


 diketahui, melalui perhitungan
diketahui, melalui perhitungan 


 adalah
adalah 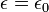 .
. adalah vektor medan listrik.
adalah vektor medan listrik. adalah
adalah
 adalah elemen diferensial volum.
adalah elemen diferensial volum.
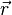 akibat adanya muatan
akibat adanya muatan  yang terletak di
yang terletak di  . Dengan demikian medan listrik di titik
. Dengan demikian medan listrik di titik 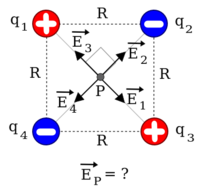

 adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik
adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik 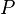 yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi
yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi  , di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa
, di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa  dan
dan  dan ambil pusat koordinat di titik
dan ambil pusat koordinat di titik  untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula
untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula





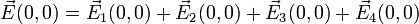

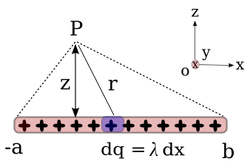
 , pada jarak
, pada jarak  di atasnya, dengan kawat merentang dari
di atasnya, dengan kawat merentang dari 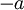 sampai
sampai 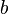 dari titik proyeksi
dari titik proyeksi 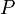 pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:
pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:![E_z = \frac{1}{4\pi\epsilon_0}\ \frac{\lambda}{z} \ \left[ \frac{b}{\sqrt{z^2+b^2}} +\frac{a}{\sqrt{z^2+a^2}} \right]](http://upload.wikimedia.org/math/e/5/c/e5c6456573df6a6c19ba66c547ba13ad.png)
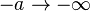 dan
dan  maka dengan menggunakan dalil
maka dengan menggunakan dalil 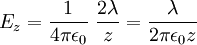
 dari kawat, dapat dituliskan medan listriknya adalah
dari kawat, dapat dituliskan medan listriknya adalah
 adalah vektor satuan radial dalam koordinat silinder:
adalah vektor satuan radial dalam koordinat silinder:
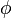 adalah sudut yang dibentuk dengan sumbu-x positif.
adalah sudut yang dibentuk dengan sumbu-x positif.
